
The calculator is pretty simple to use, whether you need it for academic or personal use, you can simply key in the digits and press enter to find the answer. It is a vector multiplication calculator for finding the cross product between two vectors. What is a Vector Cross Product Calculator? (iii) Right angles (orthogonal) to every vector in space, meaning a. (ii) Zero multiplied with any vector in space results in this property, meaning 0 ( a ) = 0. (i) An additive identity, meaning a + 0 = a. It has various forms depending upon the subject of usage. This is necessary to maintain uniformity in solving similar types of expressions all over the world. This property keeps in check the order in which expressions are supposed to be calculated and the position of parentheses in a multiple order expression. It is named after the German Mathematician, Carl Gustav Jakob Jacobi. When variables are present, we have to use the distributive property and not the standard method otherwise, we will get wrong answers. Then why are we using the distributive property? When it comes to vectors, often instead of numbers, variables are present as coefficients. If we use the standard method mentioned earlier, we would still get the answer as 24. In the above example, we observe that 2 is multiplied by 4 followed by 8, and then their resultant is added, and we get the answer 24.

Still, when it comes to distributive property, we must first multiply the numbers outside the parentheses with the numbers inside it in the proper order. Usually, while solving an expression of the above pattern, we solve the equation in the parentheses first.

It is also called the ‘Distributive Law of Multiplication and Division.’ It shows us how to find the solution to expressions like a (b + c). The anti-commutativity takes part in the coordinate notation method, and so the equalities i, j and k become -i, -j, and -k, respectively. This property primarily exhibits negative signs. There are four properties, out of which the top two are most important.

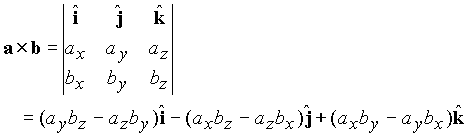
They bind the solutions of cross-products obtained. Properties play a big part in finding out cross-products of the various given vectors that layout guidelines in certain conditions.


 0 kommentar(er)
0 kommentar(er)
